1. Introduction: Biomathematics or mathematical biosciences are concerned with the applications of mathematical techniques to get an insight into the problems of biosciences. The can well be interpreted in a similar way as in engineering, physical or social science mathematics. However, situations in life sciences are quite complex and complicated and, therefore, we have to look for a situation before a mathematical model is constructed. If a model be formed, then its consequences can be deduced by using mathematical tools and the results so obtained can be compared with observations. The discrepancies between theoretical results and observations suggest further improvement of the model. The process is repeated till the model becomes a realistic one.
Biomathematics include both mathematical modeling in biology and medicine and give useful information’s to enlighten the complex biological situations. Some of the disciplines included in the subject are: botany, zoology, ecology, population dynamics, genetics, epidemiology, pharmacokinetics, physiology, environmental science and so on. The extent to which mathematics has penetrated into different disciplines varies in each instance, but with its own right in exponentially growing literature. The techniques used in biomathematics are: classical, probabilistic and statistical, computer and simulation, operations research etc.
In the present article, it is proposed to enlighten a mathematical model on population dynamics (also called demography). The field entails the study of population growth, population dispersal, effects or immigration, emigration and mixing of populations, effect of age structure on population sizes etc.
The subject is based on the populations of microorganisms so tiny in size to be seen by the naked eye. But they play an important role in (i) fermentation technology, e.g. production of alcohol, beverages, vinegar, biogas etc, (ii) mining technology like leaching out undesirable elements from ores, (iii) sanitary engineering, e.g. removal of pollutants from waste water, (iv) bioconversion of solar energy and soon. The growth difference of individual has a vital role in demography and it occurs due to space location, genetic property, age and size variations etc. of which size-difference plays a significant role due to its wide applications in fishery and forestry.
Another important consideration of population growth is the marriage in society. Kendall [1] proposed a mathematical model on this by taking the marriage rate to be constant. But the rate increases throughout the world and there exists a curvilinear relationship between the marriage rate and time. On the basis of this conception, Mishra [2] and ojha and pandey [3] modified Kendall’s model by taking the marriage rate to be a linear and quadratic function of time. However, in all these problems, the number of hermaphrodites (although a few in number) has been neglected. We, therefore, propose a model by introducing the number of hermaphrodites and taking the marriage rate to be a linear function of time.
2. The Model and Basis Equations:
Suppose M, F, H and Z denote respectively the number of unmarried males, females, hermaphrodites and married couples at any time t. $u_{1}$, $u_{2}$, $u_{3}$ are the male, female and hermaphrodite birth rates per married couples per unit time. $a_{1}$, $a_{2}$, $a_{3}$ are the death rates of unmarried male, female and hermaphrodite per unit time; $a_{4}$, $a_{5}$, $a_{6}$ are the male, female and hermaphrodite death rates per married couple per unit time. We also suppose that the marriage rate is a linear function of time t and is given by $A_{0} + A_{1}.t$, where $A_{0}$, $A_{1}$ are non-negative constant. Then the population model runs as follows: 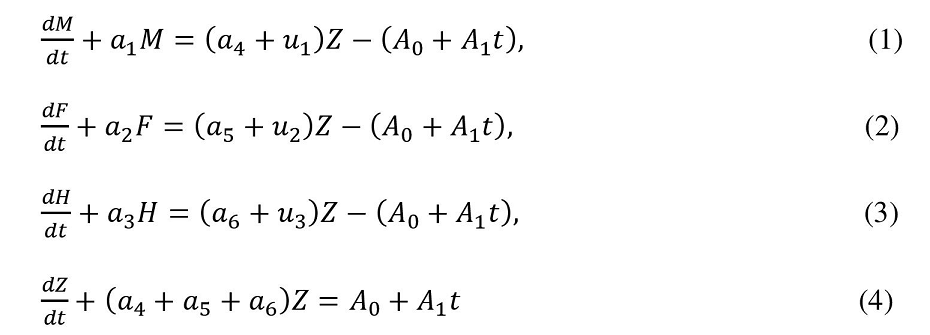
3. Solutions:
Integrating equation (4) w.r.t. $t$, we get

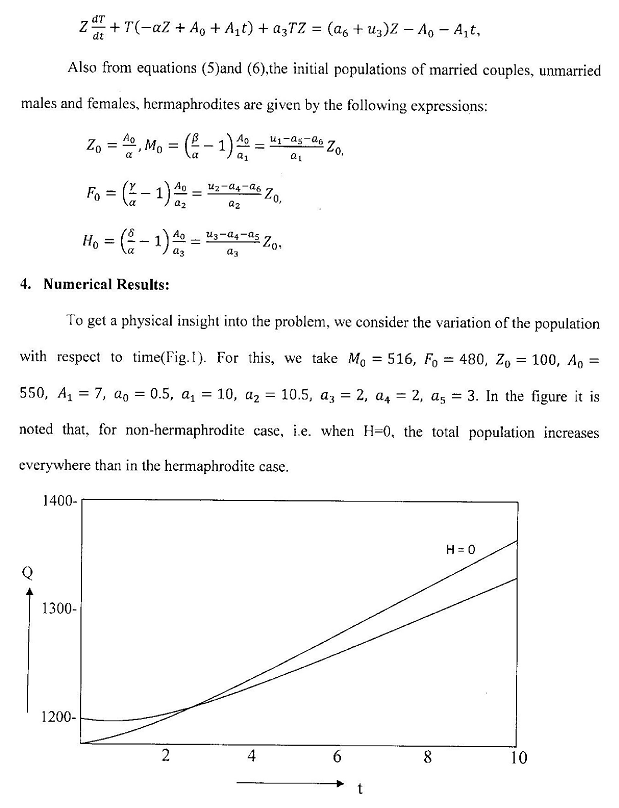
References:
[1] Kendall, D. G. : Stochastic Model and Population Growth, Demography, Springer Verlag(1977)
[2] Mishra, P. : Progress of Mathematics, Vol. 22(1988). P 20.
[3] Ojha, V.P. and Pandey, H: Jour. Nat. Acad. Math., Vol. 7(1989) p. 99
About the Author:
Dr D. C. Sanyal {Email: dcs_klyuniv[at]yahoo.com} is a retired professor of mathematics of University of Kalyani, India. Prof. Sanyal has published many research papers in several national and international journals and conferences of repute. His areas of expertise include Solid Mechanics, Hydrodynamics, Geophysics and Geidynamics and Bio Mathematics.